Why Reality has a Well-Known Math Bias

Evolution, Anthropics, and Wigner’s Puzzle

Imagine you're a shrimp trying to do physics at the bottom of a turbulent waterfall. You try to count waves with your shrimp feelers and formulate hydrodynamics models with your small shrimp brain. But it’s hard. Every time you think you've spotted a pattern in the water flow, the next moment brings complete chaos. Your attempts at prediction fail miserably. In such a world, you might just turn your back on science and get re-educated in shrimp grad school in the shrimpanities to study shrimp poetry or shrimp ethics or something.

So why do human mathematicians and physicists have it much easier than the shrimp? Our models work very well to describe the world we live in—why? How can equations scribbled on paper so readily predict the motion of planets, the behavior of electrons, and the structure of spacetime? Put another way, why is our universe so amenable to mathematical description?

This puzzle has a name: "The Unreasonable Effectiveness of Mathematics in the Natural Sciences," coined by physicist Eugene Wigner in 1960. And I think I have a partial solution for why this effectiveness might not be so unreasonable after all.

In this post, I’ll argue that the apparent 'unreasonable effectiveness' of mathematics dissolves when we realize that only mathematically tractable universes can evolve minds complex enough to notice mathematical patterns. This isn’t circular reasoning. Rather, it's recognizing that the evolutionary path to mathematical thinking requires a mathematically structured universe every step of the way.

A confused shrimp trying to figure out fluid dynamics models at the bottom of a waterfall. Generated with Gemini 2.5 Pro

The Puzzle

(Gemini 2.5 Pro summarizes Wigner’s original paper below. Readers familiar with the paper can skip below)

In his influential 1960 essay, "The Unreasonable Effectiveness of Mathematics in the Natural Sciences," physicist Eugene Wigner presented a profound puzzle that has captivated scientists and philosophers ever since. His central argument is that the success of mathematics in describing the physical world is so remarkable and unexpected that it "borders on the mysterious" and lacks any rational explanation.[1][2] He famously called it "a wonderful gift which we neither understand nor deserve."[3]

Wigner's argument can be broken down into a few key observations:

First, Wigner emphasizes that mathematics is, in his view, a human invention. It is the creation of the human mind, a formal science built on abstract concepts, rules, and "skillful operations" designed for their own sake, often for aesthetic appeal.[4] Mathematicians invent concepts with no thought to their potential application in the real world.

The core of the puzzle is that these purely abstract mathematical concepts turn out to be, time and again, perfectly suited to describe and predict phenomena in the natural world with astonishing accuracy.[1][5] Wigner argues this is "unreasonable" because there is no logical reason why the universe should obey laws that conform to man-made mathematical structures.

Wigner provides several powerful examples to illustrate this point:

• The Law of Gravitation: Isaac Newton's law of universal gravitation was formulated based on what Wigner calls "very scanty observations."[6] Yet, this simple set of equations accurately describes the motion of everything from a falling apple on Earth to the orbits of distant planets with incredible precision, far beyond what could have been reasonably expected.[5][6]

• Quantum Mechanics: Complex numbers, which include the imaginary unit i (the square root of -1), were initially considered a purely abstract mathematical curiosity.[4] Decades later, they proved to be absolutely essential to the mathematical framework of quantum mechanics, the most accurate and fundamental theory of the subatomic world.[7]

• Population Statistics: Wigner tells a short story about a statistician whose formulas for population trends surprisingly include the number π (pi).[5] His friend is baffled, remarking, "surely the population has nothing to do with the circumference of the circle."[5] This story illustrates how a concept from one area (geometry) can appear unexpectedly and effectively in a completely unrelated domain.[4]

Wigner concludes that the consistent and repeated success of abstract mathematics in physics is not a coincidence.[1] He argues that we have no rational theory for why this should be the case. The fact that a mathematical concept, developed for its own sake, later finds a perfect and precise application in a physical theory is a "miracle."[7] He leaves the puzzle unsolved, suggesting that the mystery is as profound as the existence of the laws of nature themselves or the ability of the human mind to comprehend them.

The Standard (Failed) Explanations

Before diving into my solution, it's worth noting that brilliant minds have wrestled with this puzzle. In 1980, Richard Hamming, a legendary applied mathematician¹, considered four classes of explanations and found them all wanting:

"We see what we look for" - But why does our confirmation bias solve real problems, from GPS to transistors?

"We select the right mathematics" - But why does math developed for pure aesthetics later work in physics?

"Science answers few questions" - But why does it answer the ones it does so spectacularly well?

"Evolution shaped our minds to do mathematics" - But modern science is only ~400 years old, far too recent for evolutionary selection.

Hamming concluded: "I am forced to conclude both that mathematics is unreasonably effective and that all of the explanations I have given when added together simply are not enough to explain what I set out to account for."

Enter Anthropics

Here's where anthropic reasoning comes in. Anthropics is the study of observation selection effects: how the fact that we exist to ask a question constrains the possible answers.

For example, suppose you're waiting on hold for customer support. The robo-voice cheerfully announces: "The average wait time is only 3 minutes!" Should you expect to get a response soon? Probably not. The fact that you're on hold right now means you likely called during a busy period. You, like most callers, are more likely to experience above-average wait times because that's when the most people are waiting.

Good anthropic thinking recognizes this basic fact: your existence as an observer is rarely independent of what you're observing.

Of course, the physicists and philosophers who worry about anthropics usually have more cosmological concerns than customer service queues. The classic example: why are the physical constants of our universe so finely tuned for life? One answer is that if they weren't, we wouldn't be here to ask the question.

While critics sometimes dismiss this as circular reasoning, good anthropic arguments often reveal a deeper truth. Our existence acts as a filter on the universes we could possibly observe.

Think of it this way: imagine that there are many universes (either literally existing or as a probability distribution; doesn't matter for our purposes). Some have gravity too strong, others too weak. Some have unstable atoms, others have boringly simple physics. We necessarily find ourselves in one of the rare universes compatible with observers, not because someone fine-tuned it for us, but because we couldn't exist anywhere else.

The Evolution of Mathematical Minds

Now here's my contribution: complex minds capable of doing mathematics are much more likely to evolve in universes where mathematics is effective at describing local reality.

Let me break this down:

1. Complex minds are metabolically expensive. At least in our universe. The human brain uses about 20% of our caloric intake. That's a massive evolutionary cost that needs to be justified by survival benefits.

2. Minds evolved through a gradient of pattern recognition. Evolution doesn't jump from "no pattern recognition" to "doing calculus." There needs to be a relatively smooth gradient where each incremental improvement in pattern recognition provides additional survival advantage. Consider examples across the animal kingdom:

   1. Basic: Bacteria following chemical gradients toward nutrients (simple correlation)

   2. Temporal: Birds recognizing day length changes to trigger migration (time patterns)

   3. Spatial: Bees learning flower locations and communicating them through waggle dances (geometric relationships)

   4. Causal: Crows dropping nuts on roads for cars to crack, then waiting for traffic lights (cause-effect chains)

   5. Numerical: Chimps tracking which trees have more fruit, lions assessing whether their group outnumbers rivals (quantity comparison)

   6. Abstract: Dolphins recognizing themselves in mirrors, great apes using tools to get tools (meta-cognition)

   7. Proto-mathematical: Clark's nutcracker birds caching thousands of seeds and remembering locations months later using spatial geometry; honeybees optimizing routes between flowers (traveling salesman problem)

Notice how later levels build on the previous ones. A crow that understands "cars crack nuts" can build on that to understand "but only when cars are moving" and then "cars stop at red lights." The gradient is relatively smooth and each step provides tangible survival benefits.

3. This gradient only exists in mathematically simple universes. In a truly chaotic universe, basic pattern recognition might occasionally work by chance, or because you’re in a small pocket of emergent calm, but there's no reward for developing more sophisticated pattern recognition. The patterns you discover at one level of complexity don't help you understand the next level. But in our universe, the same mathematical principles that govern simple mechanics also govern planetary orbits. The patterns nest and build on each other. Understanding addition helps with multiplication; understanding circles helps with orbits; understanding calculus helps with physics.

4. The payoff must compound. It's not enough that pattern recognition helps sometimes. For evolution to push toward ever-more-complex minds, the benefits need to compound. Each level of abstraction must unlock new predictive powers. Our universe delivers this in spades. The same mathematical thinking that helps track seasons also helps navigate by stars, predict eclipses, and eventually build GPS satellites. The return on cognitive investment keeps increasing.

5. Mathematical thinking is an endpoint of this gradient. When we do abstract mathematics, we're using cognitive machinery that evolved through millions of years of increasingly sophisticated pattern recognition. We can do abstract math not because we were designed to, but because we're the current endpoint of an evolutionary gradient that selects heavily for precursors of mathematical ability.

The Anthropic Filter for Mathematical Effectiveness

This gradient requirement is what really constrains the multiverse. From a pool of possible universes, we need to be in a universe where:

• Simple patterns exist (so basic pattern recognition evolves)

• These patterns have underlying regularities (so deeper pattern recognition pays off)

• The regularities themselves follow patterns (so abstract reasoning helps)

• This hierarchy continues indefinitely (so mathematical thinking emerges)

• …and the underlying background of the cosmos is sufficiently smooth/well-ordered/stable enough that any pattern-recognizers in it aren’t suddenly swallowed by chaos.

That's a very special type of universe. In those universes, patterns exist at every scale and abstraction level, all the way up to the mathematics we use in physics today.

In other words, any being complex enough to ask "why is mathematics so effective?" can only evolve in universes that are mathematically simple², and where mathematics works very well.

Consider some alternative universes:

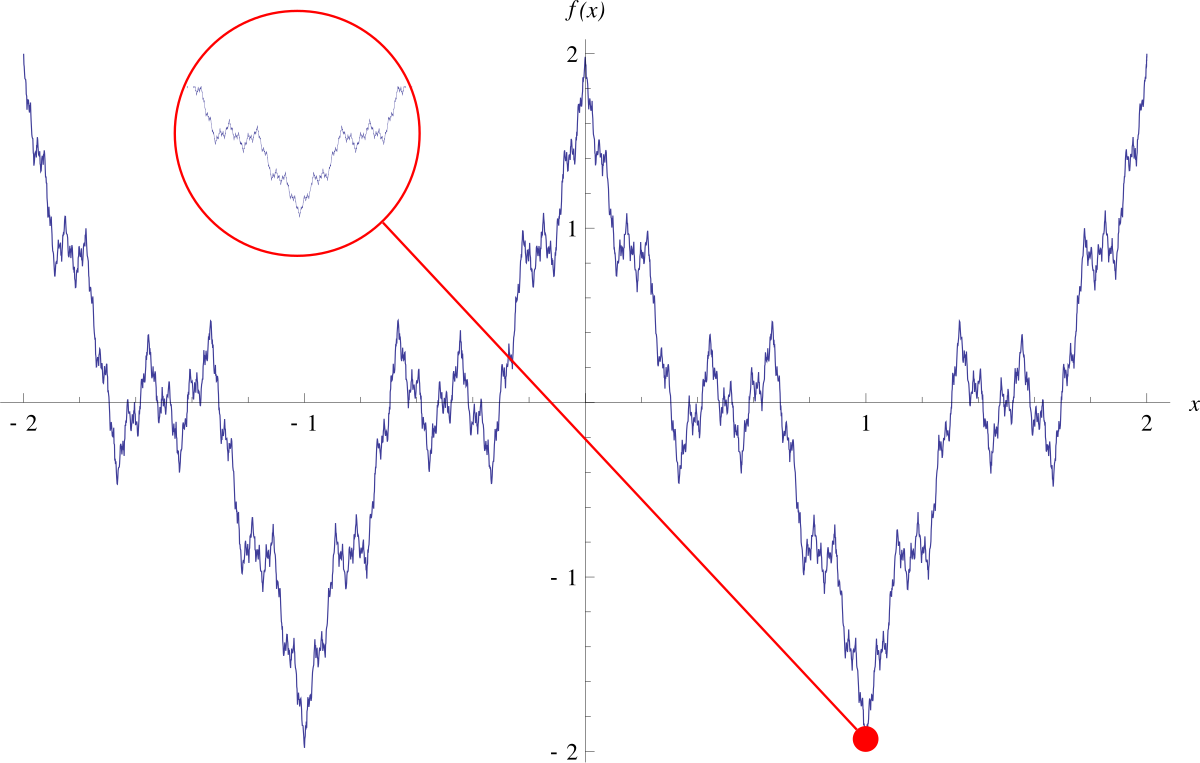
• A universe governed by the Weierstrass function (continuous everywhere but differentiable nowhere)

• A world dominated by chaotic dynamics in the formal sense of extreme sensitivity to initial conditions, where every important physical system in the world operates like the turbulence at the bottom of a waterfall.

• Worlds not governed by any mathematical rules at all. Where there is no rhyme nor reason to any of the going-ons in the universe. One minute 1 banana + 1 banana = 5 bananas, and the next, 1 banana + 1 banana = purple.

In any of these universes, the evolutionary gradient toward complex pattern-recognizing minds would be flat or negative. Proto-minds that wasted energy trying to find patterns would be selected against. Even if there are pockets that are locally stable enough for you to get life, it would be simple, reactive, stimulus-response type organisms.

The Core Reframing

To summarize, my solution reframes Wigner's puzzle entirely. Unlike Wigner (and others like Hamming) who ask "why is mathematics so effective in our universe?", we ask "why do I find myself in a universe where mathematics is effective?" And the answer is: because universes where mathematics isn't effective are highly unlikely to see evolved beings capable of asking that question.

Why This Argument is Different

There have been a multitude of past approaches to explain mathematical effectiveness. Of them, I can think of three superficially similar classes of approaches to mine: constructivist arguments, purely evolutionary arguments, and other anthropic arguments.

Contra constructivist arguments

Constructivists like Kitcher argue we built mathematics to match the reality we experience. This is likely true, but it just pushes the question back: why do we experience a reality where mathematical construction works at all? The shrimp in the waterfall experiences reality too, but no amount of construction will yield useful mathematics there. The constructivist story requires a universe already amenable to mathematical description, and minds capable of mathematical reasoning.

Contra past evolutionary arguments

Past evolutionary arguments argued only that evolution selects for minds with better pattern-recognition and cognitive ability. They face Hamming’s objection that it seems unlikely that the evolutionary timescales are fast enough to differentially select for unusually scientifically-inclined minds, or minds predisposed to the best theories.

However, our argument does not rely directly on the selection effect of evolution, but the meta-selection effect on worlds: We happen to live in a universe unusually disposed to evolution selecting for mathematical intelligence.

Contra other anthropics arguments

Unlike past anthropic treatments of this question like Tegmark, Barrow and Tipler, which focuses on whether it’s possible to have life, consciousness, etc, only in mathematical universes, we make a claim that’s at once weaker and stronger:

• Weaker, because unlike Barrow and Tipler we don’t make the claim that consciousness is only possible in finetuned universes, but a more limited claim that advanced mathematical minds are much more likely to be selected for and arise in mathematical universes.

• Stronger, because unlike Tegmark who just claims that all universes are mathematical, we make the stronger prediction that mathematical minds will predominantly be in universes that are not just mathematical, but mathematically simple.

It's not that the universe was fine-tuned to be mathematical. Rather, it's that mathematical minds can only arise in mathematical universes.

This avoids several problems with standard anthropic arguments:

• Our argument is not circular: we're not assuming mathematical effectiveness to prove mathematical effectiveness

• We make specific predictions about the types of universes that can evolve intelligent life, which is at least hypothetically one day falsifiable with detailed simulations

• The argument is connected to empirically observable facts about evolution and neuroscience

Open Questions and Objections

Of course, there are some issues to work through:

Objection 1: What about non-evolved minds? My argument assumes minds arise through evolution, or processes similar to it, in “natural universes”. But what about:

• Artificially created minds (advanced AI)

• Artificially created universes (simulation argument)

• Minds that arise through other processes (Boltzmann brains?)

My tentative response: I think the “artificially created minds” objection is easily answered; since artificially created minds are (presumably) the descendants of biological minds, or minds created some other way, they will come from the same subset of mathematically simple universes that evolved minds come from.

The “Simulated universes” objection is trickier. It’s a lot harder to reason about for me, and the ultimate answer hinges on notions of mathematical simplicity, computability, and prevalence of ancestor simulations vs other simulations, but for now I’m happy to bracket my thesis to be a conditional claim just about “what you see is what you get”-style universes. I invite readers interested in Simulation Arguments to reconcile this question!

For the final concern, my intuition is that Boltzmann brains and things like it are quite rare. Even more so if we restrict “things like it” further to “minds stable enough to reflect on the nature of their universe” and “minds that last long enough to do science.” But this is just an intuition: I’m not a physics expert and am happy to be corrected!

Evolution is such a powerful selector, and something as complex as an advanced mathematical mind is so hard to arise through chance alone. So overall my guess (~80%?) is that almost all intelligences come from evolution³, or some other referential selection pressure like it.

Objection 2: Maybe we're missing the non-mathematical patterns Perhaps our universe is full of non-mathematical patterns that we can't perceive because our minds evolved to see mathematical ones. This is the cognitive closure problem: we might be like fish trying to understand fire.

This is possible, but it doesn't undermine the main argument. The claim isn't that our universe is only mathematical, just that it must be sufficiently mathematical for mathematical minds to evolve.

Objection 3: What is the actual underlying distribution of universes? Could there just be many mathematically complex or non-mathematical universes to outweigh the selection argument?

In the post I’ve been careful to bracket what the underlying distribution of universes is, or indeed, whether the other universe literally exists at all. But suppose that the evolutionary argument provides 10^20 pressure for mathematical intelligences to arise in “mathematically simple” than “mathematically complex” universes. But if the “real” underlying distribution has 10^30 mathematically complex universes for every mathematically simple universe, then my argument still falls apart. Since it means mathematical intelligences in mathematically simple universes are still outnumbered 10 billion to one by their cousins in more complicated universes.

Similarly, I don’t have a treatment or prior for universes that are non-mathematical at all. If some unspecified number of universes run on “stories” rather than mathematics, the unreasonable effectiveness of mathematics may or may not have a cosmically interesting plot, but I certainly can’t put a number on it!

Objection 4: Your argument hinges on "simplicity," but our universe isn't actually that simple!

Is it true that a universe with quantum mechanics and general relativity is simple? For that matter, consider the shrimp in the waterfall: real waterfalls with real turbulence in fluid dynamics do in fact exist on our planet!

My response is twofold. First, it's remarkable how elegant our universe's fundamental laws are, in relative terms. While complex, they are governed by deep principles like symmetry and can be expressed with surprising compactness.

Second, the core argument is not about absolute simplicity, but about cognitive discoverability. What matters is the existence of a learnability gradient. Our universe has accessible foothills: simple, local rules (like basic mechanics) that offer immediate survival advantages. These rules form a stable "base camp" of classical physics, providing the foundation needed to later explore the more complex peaks of modern science. A chaotic universe would be a sheer, frictionless cliff face with no starting point for evolution to climb.

Future Directions

Some questions I'm curious about:

1. Can we formalize what we mean by “mathematically simple?” The formal answer might look something akin to “low Kolmogorov complexity,” but I’m particularly interested in simplicity from the local, “anthropic” (ha!) perspective where the world looks simple from the perspective of a locally situated observer in the world.

2. Can we formalize this argument further? What would a mathematical model of "evolvability of mathematical minds" look like? Can we make simple simulations (or at least gesture at them) about the distribution of possible universes and their respective physical laws’ varying levels of complexity? (See Objection 3)

3. Does this predict anything about the specific types of mathematics that work in physics?

   1. For example, should we expect physics about really big or really small things to be less mathematically simple? (Since there’s less selection pressure on us to be in worlds with those features?)

4. How does this relate to the cognitive science of mathematical thinking? Are there empirical tests we could run?

5. How does this insight factor into assumptions and calculations for multiverse-wide dealmaking through things like acausal trade and evidential cooperation in large worlds (ECL)? Does understanding that we are almost always dealing with evolved intelligences in mathematically simple worlds further restrict the types of trades that humans in our universe can make with beings in other universes?

I'm maybe 70% confident this argument captures something real about the relationship between evolution, cognition, and mathematical effectiveness. But I could, of course, be missing something obvious. So if you see a fatal flaw, please point it out!

If this argument is right, it suggests something profound: the mystery isn't that mathematics works so well in our universe. The mystery would be finding conscious beings puzzling over mathematics in a universe where it didn't work. We are, in a very real sense, mathematics contemplating itself. Not because the universe was designed for us, but because minds like ours could only emerge where mathematics already worked.

The meta-irony, of course, is that I'm using mathematical reasoning to argue about why mathematical reasoning works. But perhaps that's exactly what we should expect: beings like us, evolved in this universe, can't help but think mathematically. It's what we were selected for.

________________________________________________________

What do you think? Are you satisfied by this new perspective on Wigner’s puzzle? What other objections should I be considering? Please leave a comment or reach out! I’d love to hear critiques and extensions of this idea.

Also, if you enjoyed the post, please consider liking and sharing this post on social media, and/or messaging it to specific selected friends who might really like and/or hate on this post! You, too, can help make the universe’s self-contemplation a little bit swifter.

1. While researching Hamming’s thoughts and past works for this post, I learned a “fun” anecdote: Before the Trinity test, Richard Hamming was asked to check calculations on whether the first atomic bomb might ignite the entire atmosphere. He verified the math but was worried he didn't understand the physics enough. His friend told him not to worry, 'No one will ever blame you.'

2. What do I mean by "mathematically simple"? Not necessarily low Kolmogorov complexity from a "view from nowhere," but rather simplicity from the perspective of embedded observers. A universe might have a short description in some cosmic programming language, but if local observers can't discover or use those patterns, it doesn't matter. What matters is whether beings evolving in small patches of spacetime can discover regularities that remain true as they explore further - whether spatial exploration (from valleys to planets to galaxies) or conceptual exploration (from counting to calculus to quantum field theory).

3. For simplicity, I’m going to count “AIs descended from evolved beings” as “come from evolution,” though of course the direct selection pressure is very different. The important thing to note is that they are in the same universe as the evolved beings.